Overview
Research Area: Mathematical evolutionary biology, antimicrobial drug resistance, discrete mathematics and commutative algebra
Main project: Discrete approaches to gene interactions.
We develop discrete mathematics for analyzing sequencing data. Mutations are discrete events; a mutation occurs or not and there is no such thing as 0.3 mutations. Discrete mathematics is therefore natural for analyzing mutations. Gene interactions, or epistasis, means that the effects of mutations are not independent. For instance, the combined effect of two mutations may be substantial even if each mutation alone has only a small effect. Gene interactions are important in medicine. A double mutant bacterium can have a high degree of antibiotic resistance, even if the antibiotic works fairly well for both the corresponding single mutants. Evolutionary informed treatment strategies can reduce the problem with antimicrobial drug resistance. We have proposed antibiotic cycling strategies for hospitals (Mira et al., 2015), and it was later shown that the optimization problem we phrased, i.e., the “antibiotics time machine” problem, is NP-hard (Tran and Yang, 2017).
New biology requires new mathematics. We use graph theory, polytope theory and occasionally commutative algebra for analyzing discrete aspects of gene interactions. Our current projects depend on chromatic polynomials, Stirling numbers, Catalan numbers, Dyck words, circuits and Groebner bases. Moreover, our group (including AU students) develop code for handling large system of genotypes.
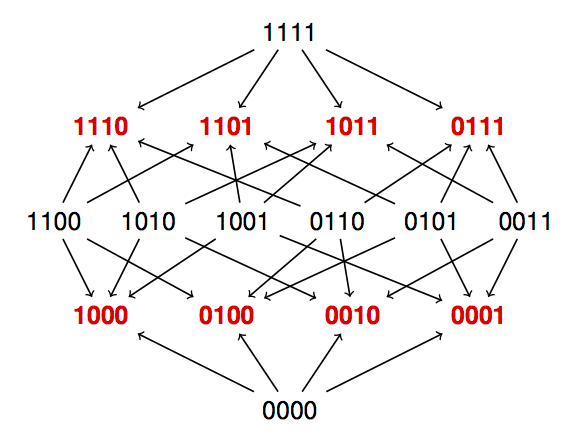
Fitness graphs
We use fitness graphs for analyzing Darwinian evolution. Each node represents a genotype, and arrows connect each pair of mutational neighbors, directed toward the node representing the genotype of higher fitness. The graphs reveal evolutionary trajectories and fitness peaks (paths and sinks of the graphs), as have been applied for relating global and local properties of fitness landscapes. In mathematical terms, a fitness graph is a cube orientation, or an acyclic cube graph. By studying fitness graph we can draw conclusions for fitness landscapes in general, rather than for a particular model, such as the NK-model. The fitness graph above has eight peaks (marked red) out of 16 nodes in total, and 50 percent is the maximal peak density for general fitness landscapes regardless of the number of loci, as observed by J. B. S. Haldane, 1931. We perform exhaustive studies of cube graphs for 3 and 4 loci in order to understand small biological systems, as well as for developing general theory.
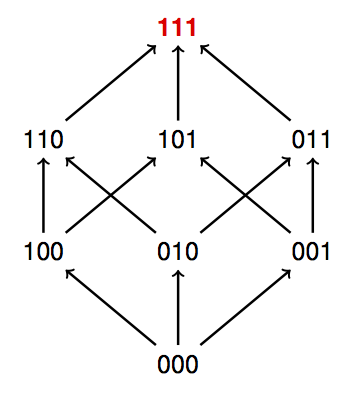
Order Perturbations and Gene Interactions
Rank orders of genotypes, from highest to lowest fitness, reveal key properties of gene interactions. Some rank orders are compatible with additive fitness. However, the proportion of such rank orders decreases rapidly by the number of loci. Each type of order perturbation that makes a rank order incompatible with additive fitness reveals some aspect of gene interactions. Order perturbations can be used for classification results and for identifying critical properties of empirical data. A fitness graph compatible with additive fitness can be presented so that all arrows point upward (see the figure above).
Student Projects
Students can get course credits for research projects, or conduct research with salary. Some students start with an independent study and continue with a stipend for summer research. Please contact me if you are interested in research projects.
Students need to fill out a registration form for an independent study. MATH-490 is the course number for independent studies. If an independent study is supposed to count as a major/minor requirement, then the grade type has to be A-F. Funding for summer research can be applied for. There are several sources and different levels of funding. It is advisable to express your interest in summer projects as early as possible in the spring.
